The Other Three Dimensions of 3DTV
Story Highlights
3DTV suggests that the three Ds are the dimensions of height, width, and depth. But there are three other linear dimensions that might be worth considering: pupillary distance, viewing distance, and screen size.
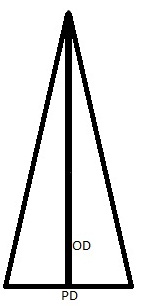 Here’s a generic diagram of binocular vision, looking down. The observer’s eyes are at either end of the short base of the triangle. The distance between the centers of the pupils of those eyes is the pupillary distance (PD, or interpupillary distance or, sometimes, interocular distance), and the distance from the object being looked at to the eyes is the object distance (OD). Each eye’s lens focuses (or tries to focus) on the object at the point of the triangle, a process called accommodation. The two eyes also point to that object, a process called vergence or convergence. And each eye sees a slightly different view, a process called stereopsis or disparity.
Here’s a generic diagram of binocular vision, looking down. The observer’s eyes are at either end of the short base of the triangle. The distance between the centers of the pupils of those eyes is the pupillary distance (PD, or interpupillary distance or, sometimes, interocular distance), and the distance from the object being looked at to the eyes is the object distance (OD). Each eye’s lens focuses (or tries to focus) on the object at the point of the triangle, a process called accommodation. The two eyes also point to that object, a process called vergence or convergence. And each eye sees a slightly different view, a process called stereopsis or disparity.
The diagram at the left might be called the plain geometry of 3D. In typical 3D shooting, two cameras replace the eyes, and the PD is replaced by a distance between lens centers, which might be the same, larger, or smaller, depending on lens magnification and the desires of the stereographer.
If the lenses are separated more than is called for in normal vision, the result is something called hyperstereo, a sensation of viewing the scene through the eyes of a giant. Distant objects that normally wouldn’t provide much of a sensation of stereopsis do, but everything seems to be closer to the observer. Hypostereo is the opposite: The lenses are closer than called for in normal vision, objects lose their stereopsis sensation at closer distances, and the overall scene depth seems greater.
That’s shooting. Now consider viewing.
Start with the PD. It’s normally considered a fixed number, and, for almost any adult human, it is. That is to say it is fixed for that one particular adult human. It varies from person to person based on age, sex, ethnicity, location, and other factors. That’s why your optician needs to measure your PD when you get a new pair of glasses, to ensure that the optical centers are where they’re supposed to be.
When I looked up “Interpupillary Distance” on Wikipedia recently, I got one range of PD figures and references; when I looked up “Pupillary Distance,” I got a somewhat different set. A 2004 paper called “Variation and extrema of human interpupillary distance” recommends that the range to be considered for adults be 45 to 80 mm. For children down to age five, the author recommends reducing the bottom end to 40 mm (and notes a 15-year-old female with a 43-mm PD). Children younger than age 2 have even smaller PDs: http://www.cl.cam.ac.uk/~nad10/pubs/EI5291A-05.pdf For the record, in September I was measured to have a PD of 68 mm.
The variation in PD poses a problem for a stereographer. To provide the sort of stereopsis and convergence I get in real life, the only PD to be considered should be 68 mm. But, if something were to be shot and presented that way and that 15-year-old female with the 43-mm PD were to view it, then, for objects at an infinite distance, for which my eyes should point straight ahead, with no convergence at all, the 15-year-old female’s eyes would diverge, an unnatural condition.
Suppose, then, that the stereographer chooses the low end of the PD range, something good enough for even five-year-olds, 40 mm. Then, when I view something at an infinite distance, instead of having my eyes point straight ahead, they’ll converge.
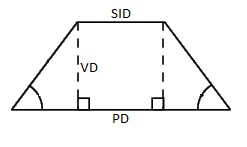 The diagram at the right shows that situation (but at an exaggerated scale). Instead of an isosceles triangle, this time the geometric figure is an isosceles trapezoid (assuming I’m pointed directly at the screen, which is a different 3D issue). In this case, the complete base is the viewer’s PD, VD is the viewing distance, and SID is the screen infinity distance, how far apart the two eye views are for the stereographer’s selected-observer PD.
The diagram at the right shows that situation (but at an exaggerated scale). Instead of an isosceles triangle, this time the geometric figure is an isosceles trapezoid (assuming I’m pointed directly at the screen, which is a different 3D issue). In this case, the complete base is the viewer’s PD, VD is the viewing distance, and SID is the screen infinity distance, how far apart the two eye views are for the stereographer’s selected-observer PD.
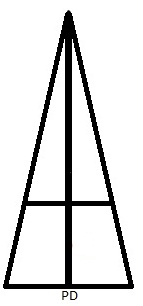 At the left, I’ve extended the sides of the trapezoid to the original triangle to show where convergence-muscle feedback puts “infinity.” Parallel lines are never supposed to meet, but the trapezoid sides aren’t parallel.
At the left, I’ve extended the sides of the trapezoid to the original triangle to show where convergence-muscle feedback puts “infinity.” Parallel lines are never supposed to meet, but the trapezoid sides aren’t parallel.
If you work out the math for an SID of 40 mm, my PD of 68 mm, and a viewing distance in a movie theater of 50 feet from the screen, the result is that the feedback that my convergence muscles send to my brain when looking at something that’s supposed to be at an infinite distance is that infinity is around 121 feet.
That might seem awfully close for a number you’re not supposed to be able to count to, but, in the grand scheme of vision, it’s not. Here’s a medical web site dealing with vision issues. Notice that the top of the page defines “infinity,” in medical visual terms, as simply greater than 20 feet: http://telemedicine.orbis.org/bins/volume_page.asp?cid=1-3-5-62
Different depth cues have different strengths at different distances. Convergence and accommodation offer strong depth cues up close, but they become relatively insignificant as viewing distances approach that medical definition of infinity, greater than 20 feet.
Viewing distance is another of those under-considered dimensions of 3DTV. In the example I gave above, I chose a viewing distance of 50 feet, not unusual for a cinema auditorium. But 3DTV is viewed at closer distances. If I were to change my viewing distance to the television-viewing Lechner Distance of nine feet, my convergence-based sensation of infinity drops to less than 22 feet — still beyond that medical definition, though I’d now be well within the range where convergence counts, leading to a stimulus conflict between stereopsis and convergence. But there’s still that third dimension, screen size.
To this point, I haven’t mentioned the screen size, because it hasn’t mattered. I’ve simply stated that the five-year-olds and I were watching whatever screen size the stereographer intended. The left- and right-eye views for something at infinite distance are separated on the screen by the 40-mm bottom of the PD range. But suppose the five-year-olds and I go to see a movie and then later bring home a 3D DVD or Blu-ray disk of the same content.
How large is the largest screen stereographers should consider? Is it 100 feet? If there’s a 40-mm SID on the screen, all of the numbers above still hold. But, if the same material, unmodified, gets put on the consumer playback medium, the ratio between the largest intended screen and the home screen becomes important.
If the largest intended screen is 100 feet and the home screen is 32 inches, then 40 mm on the giant screen becomes just over 1 mm on the home screen. If I were to sit nine feet away, my convergence-based sensation of something at infinity would put it at about nine feet away, the same as my viewing distance; it would hardly be behind the screen at all. And it’s not just objects at “infinity” that matter.
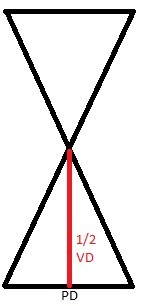 At right is yet another diagram. This time, suppose that there is a negative parallax on the screen matching the viewer’s PD. Negative parallax indicates that the right-eye view is to the left of the left-eye view. It’s easy to see from the diagram that the object appears to come out of the screen by half of the viewing distance. But what is that distance?
At right is yet another diagram. This time, suppose that there is a negative parallax on the screen matching the viewer’s PD. Negative parallax indicates that the right-eye view is to the left of the left-eye view. It’s easy to see from the diagram that the object appears to come out of the screen by half of the viewing distance. But what is that distance?
Suppose what’s coming out of the screen is an arm, from shoulder to hand. If the viewer is sitting four feet from a TV screen, the arm is a reasonable two feet long. If the viewer is sitting 50 feet away from a cinema screen with the same negative parallax, the same arm becomes 25 feet long.
Perhaps other visual scaling factors come into play in such situations. After all, when we see a close up on a 2D movie screen, we don’t suddenly think the character is a gigantic monster. But the multiple dimensions of 3DTV seem to complicate matters.
Some have proposed an alternative. In one paper, it has been called “Just Enough Reality” (http://www.cs.cmu.edu/afs/cs/user/mws/ftp/papers/t3dvt99-final.pdf). In another, it’s called “Kinder Gentler Stereo” (http://www.ri.cmu.edu/pub_files/pub1/siegel_mel_1999_1/siegel_mel_1999_1.pdf).
The technical term is microstereopsis. The “bad” news about it is that it doesn’t exactly duplicate the top triangle in this post. But, thanks to variation in human PD as well as varying viewing distances and screen sizes, it’s unlikely that any real-world 3DTV system will match that triangle.
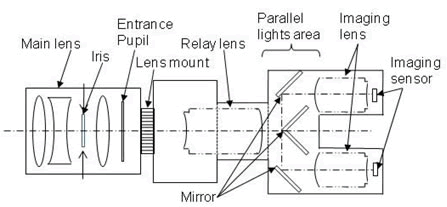 The good news is that microstereopsis doesn’t necessarily require two lenses per 3D position. Some of the 3D that Sony showed at the 2009 Consumer Electronics Show was shot with a single-lens microstereopsis camera (the one that drew much interest at the CEATEC show last year). But an older system (shown in the 1970s by Digital Optical Technology Systems) didn’t require even a camera with dual image sensors.
The good news is that microstereopsis doesn’t necessarily require two lenses per 3D position. Some of the 3D that Sony showed at the 2009 Consumer Electronics Show was shot with a single-lens microstereopsis camera (the one that drew much interest at the CEATEC show last year). But an older system (shown in the 1970s by Digital Optical Technology Systems) didn’t require even a camera with dual image sensors.
Microstereopsis might turn out to be a bad idea — or it might be a good one. Despite the 82 years since the first 3DTV broadcast, it’s still a young field.
